Ano/Série
9° ano ensino fundamental
9° ano ensino fundamental
Objetivo
Possibilitar aos alunos um melhor entendimento sobre o ensino da função quadrática e construir gráfico com o uso do GeoGebra.
Desenvolvimento
Função Quadrática
Chama-se função quadrática, ou função polinomial do 2º grau, qualquer
função f de IR em IR dada por uma lei da forma f(x) = ax² + bx + c, onde a, b e
c são números reais e a 0.
Exemplos
Exemplos
1. f(x) = 3x2 - 4x + 1, onde a = 3, b = - 4 e c = 1
3. f(x) = 2x2 + 3x + 5, onde a = 2, b = 3 e c = 5
4. f(x) = - x2 + 8x, onde a = -1, b = 8 e c = 0
5. f(x) = -4x2, onde a = - 4, b = 0 e c = 0
Gráfico
Gráfico
O gráfico de uma função polinomial do 2º grau, y = ax² + bx + c, com a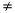 0, é uma curva chamada
parábola.
0, é uma curva chamada
parábola.
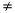 0, é uma curva chamada
parábola.
0, é uma curva chamada
parábola.
Exemplo
Vamos construir o gráfico da função y = x² + x:
Primeiro atribuímos a x alguns valores, depois calculamos o valor
correspondente de y e, em seguida, ligamos os pontos assim obtidos.
Observação
Ao construir o gráfico de uma função quadrática y = ax² + bx + c,
notaremos sempre que:
se a > 0, a parábola tem a concavidade voltada para cima;
Zero e Equação do 2º Grau
Chama-se zeros ou raízes da função polinomial do 2º grau f(x) = ax² + bx +
c , a 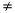 0, os números reais x
tais que f(x) = 0.
0, os números reais x
tais que f(x) = 0.
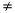 0, os números reais x
tais que f(x) = 0.
0, os números reais x
tais que f(x) = 0.
Então as raízes da função f(x) = ax² + bx + c são as soluções da equação
do 2º grau ax² + bx + c = 0, as quais são dadas pela chamada fórmula de
Bhaskara:
A quantidade de raízes reais de uma função quadrática depende do valor
obtido para o radicando 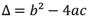 chamado discriminante, a saber:
chamado discriminante, a saber:
* Quando é positivo, há duas
raízes reais e distintas;
é positivo, há duas
raízes reais e distintas;
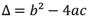 chamado discriminante, a saber:
chamado discriminante, a saber:* Quando
 é positivo, há duas
raízes reais e distintas;
é positivo, há duas
raízes reais e distintas;
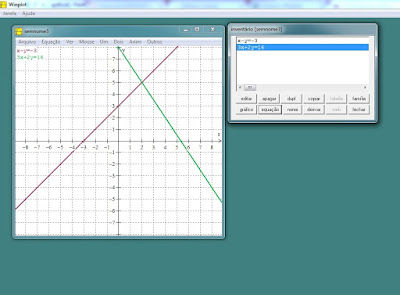
Software GeoGebra
É um software gratuito, disponível em português, desenvolvido para
facilitar o ensino da matemática, englobando todos os níveis de aprendizagem,
foi criado em 2001 por Markus Hohenwarter.
Por se tratar de um aplicativo de geometria dinâmica, o aluno pode manipular objetos e figuras já prontas, e também construir instrumentos para as suas observações. Os saberes matemáticos vão sendo por ele assimilados, na medida em que movimentam as construções e observam suas características.
Por se tratar de um aplicativo de geometria dinâmica, o aluno pode manipular objetos e figuras já prontas, e também construir instrumentos para as suas observações. Os saberes matemáticos vão sendo por ele assimilados, na medida em que movimentam as construções e observam suas características.
Link para download GeoGebra
Dicas para aprender a usar o software AQUI
Explorando o GeoGebra
Segue o LINK para você explorar o software e na sequência fazer suas atividades.
Atividade
1) Para construir um cercado retangular para seu cachorro, João dispõe de
36 metros de tela. Na construção, ele pretende utilizar toda a tela e
aproveitar um muro como um dos lados do cercado, como mostra na figura.
a) Escreva uma fórmula que relacione a área A do cercado em função da
medida x indicada?
b) Construa o gráfico da função que você escreveu no item a.
c) Qual a maior área que pode ter esse cercado?
d) Quais devem ser as dimensões desse cercado para que se
possa obter a maior área?
2) Dada a função quadrática f(x) = -2.x² + 4.x – 9, as coordenadas do
vértice do gráfico da parábola definida por f(x), é:
3) O transporte aéreo de pessoas entre duas cidades A e B
é feito por uma única companhia em um único voo diário. O avião utilizado tem
180 lugares, e o preço da passagem p relaciona-se com o número x de passageiros
por dia pela relação p = 300 – 0,75x. Qual a receita máxima possível por
viagem?
a) R$ 30.000,00
b) R$ 29.700,00
c) R$ 29.900,00
d) R$ 29.600,00
e) R$ 29.800,00
Conclusão
O software aparece como um meio de auxiliar na aprendizagem, com o
objetivo de promover um ensino lúdico e dinâmico, estimulando a memória gráfica
e a inteligência visual, corrigindo as dificuldades encontradas pelos alunos no
estudo das funções.
Assim, é possível perceber o quanto é necessário e importante o professor
de matemática identificar nos seus alunos o elevado grau de desempenho,
competências e habilidades para a desenvoltura de exercícios matemáticos.
Referências
Site Só Matemática